Dan Hicks
Thursday, 25 March, 1999
Math 232, Smith
Hyperspace: An Introduction to the Fourth Dimension
One of the nicest things about linear algebra is the ease with which we may work in any number of variables. Working with three or more dimensions comes naturally in areas where math is used for practical purposes: for example, in economics, supply-and-demand calculations for a single corporation may involve hundreds of quantities. But thinking about four variables as four dimensions is a much more difficult, much more intriguing, and fairly recent idea. The easiest way to begin thinking about how four dimensions looks is to consider how three dimensions would appear to two-dimensional beings, and so we shall begin there and then move on to four dimensions.
The idea of two-dimensional beings, living in and perceiving only a plane, goes back at least as far as Plato, with a race of men whose sole experience is shadows on the walls of caves; to them, the truth would be literally nothing but the shadows of the images. One of the first really intriguing works of fiction about two-dimensional beings is the famous Flatland, written by Edwin Abbott in 1884. In it, a two-dimensional Flatlander appropriately named A Square is inducted into the wonders of the previously unknown three dimensions by A Sphere (who, not coincidentally, is a sphere). (Ironically, Abbott was not a mathematician, but an ordinary Victorian schoolmaster).
A Sphere first appears to A Square by passing through the plane of Flatland: as near as A Square can tell, in his locked room, there appears a point, which inexplicably grows to a circle, swells, then just as mysteriously shrinks down to nothing. We, of course, can picture what really happened in three dimensions (Fig. 1). As an introduction to four dimensions, we could be visited by a hypersphere, and we would see something similar to what A Square saw: a point would appear suddenly, grow into a sphere, then shrink down again to a point just before vanishing (Fig. 2).
But using our imaginations, we should be able to work with four dimensions more directly than the way they appear in intersecting our three dimensions. Let us begin by constructing a hypercube, then use that as a basis for four axes. We start with a point; move the point in one direction and leave a trail and you have a line. Move the line in another, perpendicular direction, and you have a square. Move the square in a third, still perpendicular direction, and you have a cube (Fig. 3). Now for the tricky part, the part we can’t draw well: imagine displacing the cube in a fourth direction, and the resulting figure will be a hypercube. We can imagine this fourth direction in a few ways: to a side we haven’t moved the figures through yet (Fig. 4), or, as we may imagine a drawing of a cube as a square-in-a-square, as a cube-within-a-cube (Fig.5). Personally, I prefer a sense of moving behind (Fig. 6; the arrows point in the direction of the movement).
Now, using the lines from our hypercube, we can
construct a set of coordinate axes in four dimensions. We follow a similar
procedure: picking a point at the origin, we move a point along each of
the first three axes in turn, then pick another direction for the fourth
(Fig. 7). Now, let’s try our hand at doing a fairly simple geometric
problem. Our task: to find the matrix for the linear transformation of the
reflection through the hyperplane x=z.
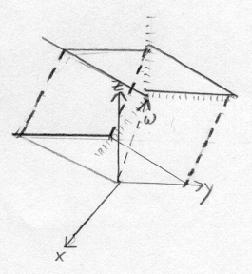
We start as we would with any other geometric problem: with a picture
(Fig. 8). Now we imagine the standard basis vectors,
![]() and how they each are
changed in the reflection, and see that
and how they each are
changed in the reflection, and see that ![]() and
and ![]() , which correspond to
the x and z axes, are reflected into each other’s
positions, while the other vectors are left unchanged.
, which correspond to
the x and z axes, are reflected into each other’s
positions, while the other vectors are left unchanged.
Then constructing the matrix A of the transformation is easy:
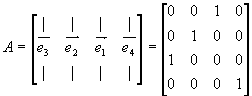 .
.
There are many more interesting constructs to be explored in four-dimensional geometry, such as: "Any two points are equidistant from each other, and an equilateral triangle is three points in two dimensions that are all equidistant. A regular tetrahedron is four points in three dimensions with the same characteristic; what would a similar construct in four dimensions look like?" but I don’t doubt that the reader new to thinking about four dimensions has a headache, so I will leave with this advice for them: don’t worry if you can’t quite manage the pictures this time; I’ve been thinking about the way four dimensions look for nearly a decade, ever since I read Flatland for the first time, and I haven’t made much more progress than what I cover here. Perhaps we’ll only be able to really work with four-dimensional geometry when we’ve developed faster holography, or something similar; we simply lose too much information when we try to draw four-dimensional figures on flat surfaces.
Fig. 1, from The Fourth Dimension by Rudy Rucker.

Fig. 2, from The Fourth Dimension by Rudy Rucker.
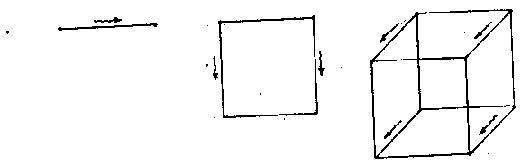
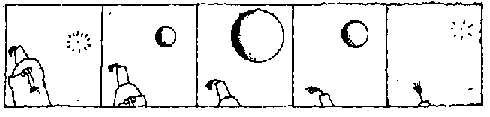 Fig.
3, from The Fourth Dimension by Rudy Rucker.
Fig.
3, from The Fourth Dimension by Rudy Rucker.
Fig 4., from The Fourth Dimension by Rudy Rucker.
Fig. 5, from The Fourth Dimension by Rudy Rucker.
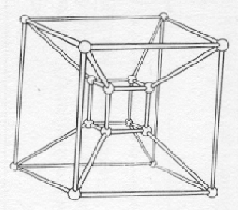 Fig. 6, drawn by the
author.
Fig. 6, drawn by the
author.
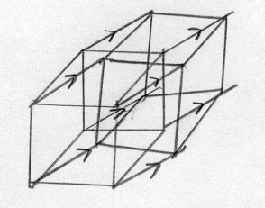
Fig. 7, drawn by the author.
Fig. 8, drawn by the author.
1. "variables": I will be using the terms variable and dimension interchangeably, in the sense that having three variables is the same as working in three dimensions.
2. "shadows of the images": Plato, The Republic.
3. "hypersphere": When we talk about ojects in four dimensions that are similar to two- and three- dimensional objects, we give them the prefix hyper- and assume they can be constructed by the same definition as in three dimensions (i.e., a hypersphere is the collection of all the points in four dimensions that are a certain distance from a fixed point).
4. "hyperplane x=z": Here I use the convention that a four-dimensional coordinate system uses the letters x, y, z, w.
References
Abbott, Edwin Abbott. Flatland, A romance of many dimensions. New York: Barnes and Noble, 1963.
Manning, Henry P., Ph.D. (ed.). The fourth dimensions simply explained. New York: Munn & Company, Inc., 1910.
Rucker, Rudy. The fourth dimension: A guided tour of the higher universes. Boston: Houghton Mifflin Company, 1984.
---------------. Geometry, relativity, and the fourth dimension. New York: Dover Publications, 1977.